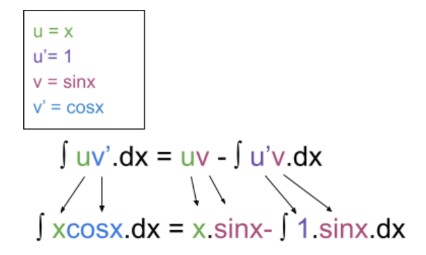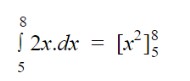İntegrallere Giriş: Tanım, Kurallar, Örnekler ve Çözüm
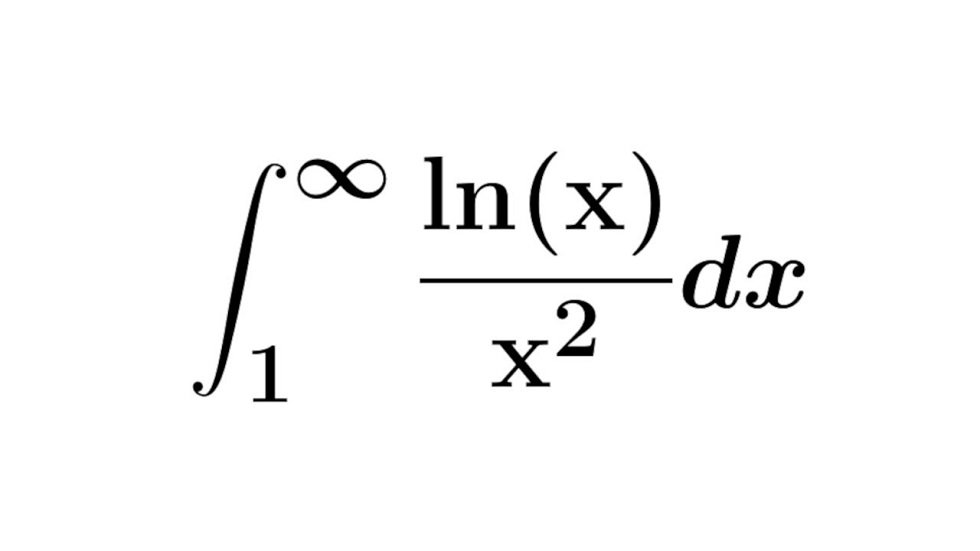
Bir grafik üzerinde düz bir çizginin altındaki alanı farklı formüllerle bulabiliriz. Ama bir eğri çizgisinin altındaki alanı nasıl bulacağınızı hiç merak ettiniz mi? Çünkü evet ise endişelenmeyin, aynı sayfadayız.
Bir eğri doğrunun eğimini türev yoluyla hesaplayabileceğimizi zaten biliyoruz. Şimdi, bir eğri çizgisinin altındaki alanın formülünü bulmaya çalışalım.
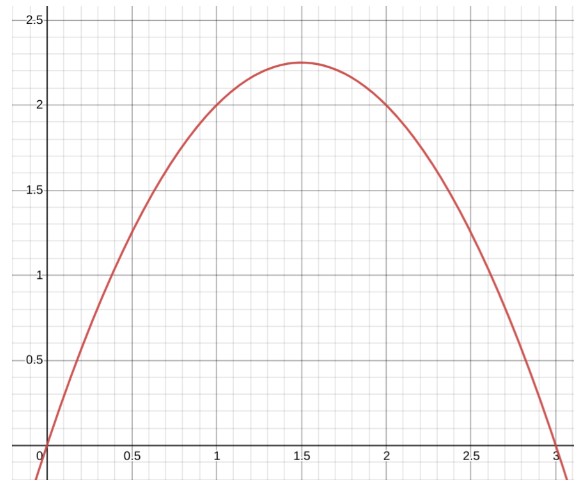
Daha iyi anlamak için bu grafiği göz önünde bulundurun.
X ekseni üzerinde ve üzerinde 0'dan 3'e kadar olan eğrinin altındaki alan nasıl hesaplanabilir?
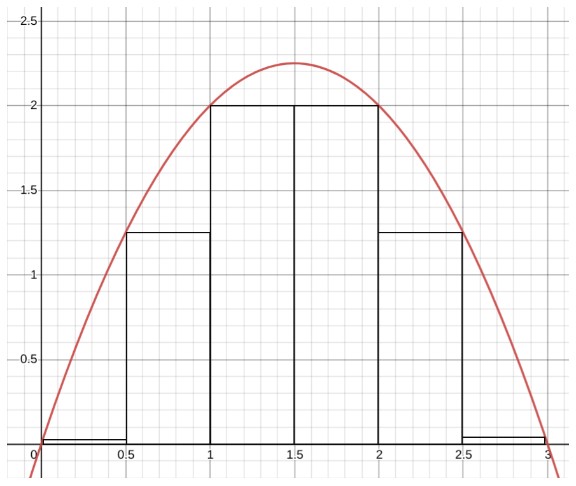
Riemann'a göre, eğri çizgisinin altındaki belirli dikdörtgenlerin alanının toplamı, o eğrinin altındaki yaklaşık alanı verir. Bunun gibi bir şey:
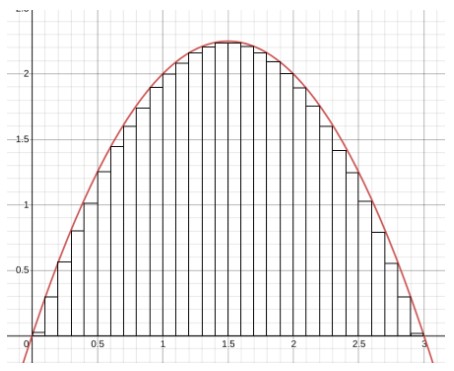
Ancak bu yeterince tatmin edici değil. Dikdörtgen levhaların genişliğini azaltmaya ne dersiniz? Ve biraz daha ve biraz daha. Belki böyle:
Bu alan bir öncekinden nispeten daha doğru olacaktır. Ama ya eğer... Biraz daha azaltıyoruz. O kadar ki neredeyse sıfır! Aklına bir şey mi geldi?
EVET, Türevler! Türevler anlık eğimi hesaplamak için kullanılır. Bu eğrinin altındaki alanı bulmak için bu kavramı kullanacağız. Bu kavrama integral denir.
İntegrallerin ne olduğunu öğrenelim mi? İntegrallerin kuralları nelerdir ve nasıl çözülür?
İntegraller nedir?
İntegral, integralleri bulma sürecidir. İntegrallerin hacim bulma, kütle vb. gibi birçok uygulaması vardır, ancak bu yazıda bir eğrinin altındaki alanı tartışacağız.
İntegralin tanımı:
"Bir fonksiyonun türevi f'(x) ise, integrali ∫f(x).dx + c'dir."
Bu bir örnekle açıklanabilir. Bir fonksiyonu ve türevini düşünün, yani f'(x) = 3. Ama antitürevi nedir? Bazı varsayımlarda bulunabiliriz.
Düşünürseniz, tek bir X'e sahip bir fonksiyon için türev olarak sabit bir terim elde ederiz. Yani:
= 3x
Böylece, orijinal işlevi 3x antidiferansiyasyon ile elde ederiz.
İntegral Katsayısı
Şu denklemlere bakın:
- 3x + 12
- 3x + 100
Tüm bu denklemlerin türevi de 3x'tir. Bu yüzden herhangi bir hatayı gidermek için şunu yazıyoruz:
= 3x + C burada c herhangi bir sabit sayı olabilir
Bu nedenle integral, bu fonksiyonun tüm olası ters türevlerine sahiptir.
Artık integralin ne olduğunu bildiğinize göre, şimdi integral gösterimini öğreneceğiz.
İntegral Gösterimi
Her işlemin bir operatörü, bir sembolü vardır. Türevler için d/dx gösterimimiz var. Benzer şekilde, integraller için süslü bir s kullanırız.
∫ fx.dx + c
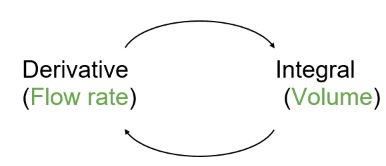
İntegraller ve Türevler
"Artık integralin ne olduğunu biliyorum ama türevlerle nasıl bir ilişkisi var?" diye merak edebilirsiniz.
Kesin olmak gerekirse, Antitürevler ( ters türev ) ve belirsiz integraller hemen hemen aynı şeylerdir. Ancak belirli integraller ve karşıt türevler arasında büyük bir fark vardır.
Türevleri bulduğumuzda, iki nokta arasındaki farkı o kadar düşürürüz ki, sonsuz küçük olur. Ancak integrallerde o kadar çok küçük parça yaparız ki, bunların sayısı sonsuza ulaşır.
Basit bir deyişle, türevlerde yaklaşık sıfır değerinin sınırını uygularız ve integralde sınırı sonsuza uygularız. Yani integrallerin ters türevler olduğunu söyleyebiliriz.
İntegrallerin Kuralları
İntegralleri, türev kurallarını kullandığımız gibi çözmeye yardımcı olan bazı kurallar vardır. İntegral kuralları, türevleri çözmek için kullandığımız kurallarla oldukça ilişkilidir.
Güç Kuralı
Bir işlev belirli bir güce yükseltildiğinde, entegrasyon için kullanılan kural şu şekildedir:
∫ fx.dx = (xn+1)/n+1
Farklılaşmanın güç kuralından türetilmiştir. Önce bu kuralın farklılaşma için güç kuralının tersi olduğunu kanıtlayalım.
Örnek
Bir fonksiyonun türevi 6x 2'dir. Farklılaşma sürecini gözden geçirelim ve tam tersini yapalım.
- Bir fonksiyonun kuvvetinden bir çıkarılır, bu yüzden tersini bulmak için kuvvete bir ekleriz, yani 6x 2+1 = 6x3.
- Katsayı güçle aynıdır, bu yüzden tersine çevirmek için aynı sayıya böleceğiz, yani 6x 3/3 = 2x 3.
Yani 6x 2'nin integrali 2x 3'tür ( orijinal fonksiyon ). 2x 3'ün türevinin 6x 2 olup olmadığını doğrulamak için türev hesaplayıcıyı kullanın.
Sabit ile çarpılır
Sabit bir sayı ile çarpımda olan bir fonksiyon gördüğümüzde bir kural uygularız. Bu kurala göre, integral sırasında sabit terim integral gösteriminden çıkarılır.
∫k.fx dx =ck ∫fx dx
Örnek
Bir fonksiyon f(y) = 6y2 + 12y'dir. 6 ve 12 sabit sayılarını görebilirsiniz. 6 ortak ele alalım.
= 6 ( y2 + 2y)
Entegrasyonu uygula:
∫ 6y2 + 12y .dy = 6 ∫ y2 + 2y .dy
Güç kuralının uygulanması:
= 6 ∫ y2 + 2y .dy
= 6 { (y2+1)/2+1 + 2y1+1/1+1 }
= 6 { y3/3 + y2}
= 2y3 + 6y2 + c
Toplama Kuralı
İki fonksiyon eklendiğinde, entegrasyon sırasında ayrı ayrı entegre edilebilir ve daha sonra eklenebilir.
∫ (fx + gx).dx = ∫ fx.dx + ∫ gx.dx
Örnek
u5 + 2u'nun integralini bulun.
Çözüm:
∫u5 + 2u.du = ∫u5.du + ∫2u.du
= (u5+1/ 5+1) + 2∫u.du
= u6/6 + 2u1+1/2
= u6/6 + u2 + c
Fark Kuralı
Toplam kuralına benzer şekilde, fonksiyonlar çıkarma aşamasındayken, ayrı ayrı entegre edilebilirler.
∫ (fx - gx).dx = ∫ fx.dx - ∫ gx.dx
Örnek
u5 - 2u'yu bulun.
Çözüm:
∫u5 + 2u.du = ∫u5.du - ∫2u.du
= (u5+1/ 5+1) - 2∫1u.du
= u6/6 - 2u1+1/2
= u6/6 - u2 + c
Yukarıdaki örnekten de görebileceğiniz gibi, toplam ve fark kuralı arasındaki tek fark işaret sembolüdür.
Parçalara Göre Entegrasyon
Farklılaşmanın ürün kuralının tersidir. Formülünü türetelim.
Ürün kuralı şudur:
(uv)' = uv' + u'v
Her iki tarafa da entegrasyon uygulayın.
∫(uv)'.dx = ∫ uv'.dx + ∫ u'v.dx
uv = ∫ uv'.dx + ∫ u'v.dx
∫ uv'.dx = uv - ∫ u'v.dx
Örnek
∫ x.cosx .dx değerlendirin
Çözüm:
u ve v'yi tanımlayın.
u = x
v' = cosx
u' ve v değerlerini bulun.
u' için u 'nun türevini bulunuz.
u = x
u' = 1
v için, v' nin integralini bulun.
v = cosx
∫v.dx = ∫ cosx.dx = sinx
Çözmek.
∫xcosx.dx = x.sinx - ∫1.sinx.dx
= x.sinx - cosx
Sabit ekle'yi tıklayın.
= x.sinx - cosx + c
İkame Kuralı
Bu kural aynı zamanda ters zincir kuralı olarak da bilinir. Bu kural özel durumlarda uygulanır. Bazen işlev, değiştirme kuralının uygulanabileceği şekilde ayarlanabilir.
Kural şudur:
∫ f((gx)).g'(x).dx = ∫f(u).du
Bu formülü anlamak için ilgili işlemlere bakın.
g'(x) = d/dx g(x)
Kolaylık sağlamak için, izin verin
u = g(x) o zaman du = g'(x)
Bu formülün yalnızca entegre edilecek fonksiyonda hem u hem de u' olduğunda geçerli olduğu unutulmamalıdır.
Örnek
(x + 1)2'in integralini bulunuz.
Çözüm:
Fonksiyonu anlayarak x + 1'in türevinin 1 olduğunu görebiliriz . Bu, ikame kuralını kullanmak için 1'i çarpabileceğimiz anlamına gelir.
∫(x + 1)2.dx = ∫(x + 1)2.1dx
Şimdi sırasıyla x + 1 ve 1 olan sen ve sen var. Formülü kullanarak:
∫(x + 1)2.1dx = ∫ u2. du
= ∫ u2+1 / 3
= ∫u3/3
Değerinizi geri koymak:
= ∫(x+3)3 / 3
Diğer Bazı Kurallar
|
Fonksiyon |
İntegral |
|
∫cos(x).dx |
sinx + c |
|
∫sin(x).dx |
-cosx + c |
|
∫sec2(x).dx |
tan + c |
|
∫(1/x).dx |
ln|x| + c |
|
∫ex . dx |
ex + c |
|
∫ln(x).dx |
x ln(x) - x + c |
İntegral Türleri: Belirsiz ve Belirli İntegraller
İki tür integral vardır. Her ikisi de farklı şekilde çözülür ve farklı uygulamalara sahiptir.
Belirsiz İntegraller
Bir türevin tersidir. Bir eğri çizgi grafiğinin altındaki tüm alanı hesaplar. Şimdiye kadar bu makalede gördüğünüz tüm örnekler belirsiz entegrasyondur.
Bu integrallerde alt ve üst sınır limitleri uygulanmaz. Ayrıca, cevabın fonksiyonun tüm olası antitürevlerini içerdiğini belirtmek için sonuna bir sabit c eklenir.
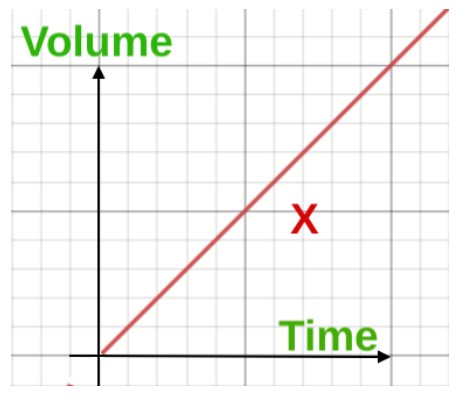
Bir havuz örneğini ele alalım. Havuzu bir su borusu yardımıyla doldurduğunuzu düşünün. Su akışı bazı nedenlerden dolayı ara sıra değişiyor.
Şimdi, akış hızı tutarlı olsaydı, bir süre sonra havuzdaki su hacmini hesaplamak kolay olurdu.
Ancak sorun şu ki, akış hızı sürekli değişiyor ve sadece bir noktada ölçülemiyor. Tam hacmi bilmek için her noktada akış hızını bulmak gerekir.
Bu amaçla belirsiz integraller kullanıyoruz. Akış Hızı türevler tarafından hesaplanır ve t anında havuzun hangi oranda dolduğunu söyler.
d/d (x2) = 2x ( akış hızı )
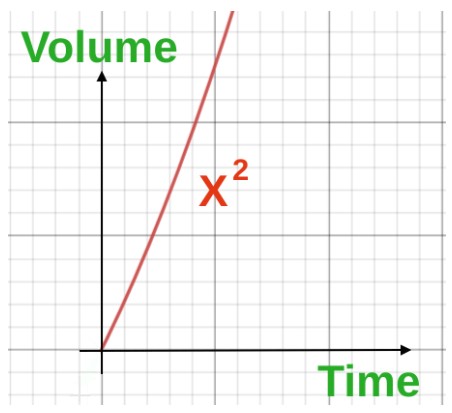
Entegrasyon, t zamanından sonra havuzdaki suyun hacminin ne olduğunu söyler.
∫2x.dx = x2 ( cilt )
Bu aynı zamanda integrallerin antitürev olduğu gerçeğini de doğrular.
Şimdi, ya havuzda zaten biraz su varsa? Bu, hesaplanan hacmimizin "net hacim" olmadığı anlamına gelir. Doğru cevabı almak için cevaba c ekleyin.
= x2 + c
Belirli İntegraller
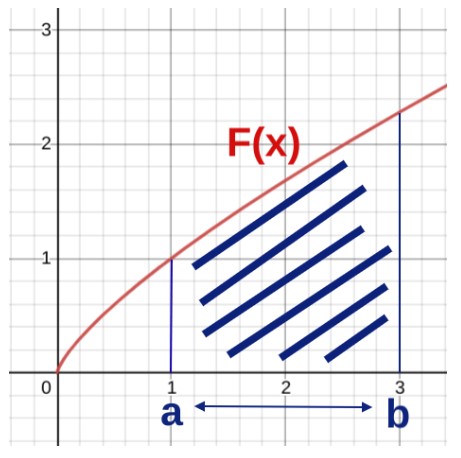
Belirli integral, hacmi belirli bir zaman aralığında bulur. Örneğin, x ekseninde a ve b noktaları arasında biriken hacmi hesaplamak istiyorsunuz.
X ekseninde 1 ile 3 arasındaki alanı hesaplamak için üst ve alt sınır sınırlarını uygularız. Bu şekilde, vurgulanan kısmın tam kesin alanını bulacaksınız.
Havuz örneğinden devam edersek, 5. dakika ile 8. dakika arasında havuza eklenen suyun hacmini bulmak istediğimizi varsayalım. Yazacağız:
Fonksiyonu entegre ettikten sonra, sırasıyla a ve b değerlerini koyun ve b değerini a değerinden çıkarın.
= [(8)2 - (5)2]
= 64 - 25
= 39
Ters türev hesaplayıcı, belirli bir fonksiyon için hem belirli hem de belirsiz integralleri bulabilir.
İntegraller, bir eğrinin altındaki alanı bulmak için kullanılır. Şık S sembolü ile temsil edilir . İntegral kuralları entegrasyon sürecinde yardımcı olur. İntegraller belirli veya belirsiz olabilir ( antitürevler ).